calculation
data
plotting
Code 
try:
    import fysisk_biokemi
    print("Already installed")
except ImportError:
    %pip install -q "fysisk_biokemi[colab] @ git+https://github.com/au-mbg/fysisk-biokemi.git"

Python: Calculations

Code 
import numpy as np

(a) Simple calculations

Evaluate the following expressions using Python

  • \(10.5 \times 4\)
  • \(5 + 10 + 15 + 12\)
  • \(70 - 30 + 2\)
  • \(420 / 10\)
... # Replace ... with your code
...
...
...
Tip

Recall that the basic arithemetic operations are, in Python, represented as follows

  • \(+ \Rightarrow\) +
  • \(- \Rightarrow\) -
  • \(/ \Rightarrow\) /
  • \(\times \Rightarrow\) *
  • \(x^y \Rightarrow\) x**y

(b) Array calculations

The cell below defines an array \(a\) with all the numbers from 0 to 9.

For each entry \(a_i\) in the array calculate the expression \(b_i = a_i / 3 + a_i^2\) and assign that to a new array \(b\). use the fact that you can do elementwise operations with an array - do not calculate it seperately for every element of the array.

a = np.arange(0, 10)
b = ...
print(b)
Tip

With an array all the basic arithemtic operations can do be done elementwise, so the expression \(x^2 + 1\) can be done for all elements in an array as such

x = np.arange(0, 10)
y = x**2 + 1

Just like if x was just a single number. Similarly, expressions be involve adding arrays together like

y = x**2 + x

(c) Variables

Variables are an essential part of a program. Calculate the following where each intermediate is assigned to a variable

\[ \begin{aligned} a &= 5 \times 3 \\ b &= a + 9 \\ c &= \frac{4}{3}a + b + 2 \end{aligned} \]

a = ...
b = ...
... 
print(a, b, c)

Bonus question: Why does c print as a decimal number when the others print without decimals?

(d) Parentheses

Parentheses a very important, one misplaced parentheses and the universe could have been drastically different - if parenthesis had been missing it is likely the universe would never have existed.

Using the variables a, b and c you calculate in the previous exercise, evaluate the following expressions

  • \(a \times (b + c)\)
  • \(a \times b + c\)
  • \(\frac{a + b + c}{b + c}\)
  • \((b - a)(\frac{1}{c} + 1)\)
  • \((b - a)(\frac{1}{c+1} + 1)\)
q1 = ...
q2 = ...
q3 = ...
q4 = ...
q5 = ...
print(q1, q2, q3, q4, q5)

(f) Functions

For repeated computations it’s good practice to define a function. Define a function that calculates the following expression

\[ f(x) = \frac{Ax + B + C}{A + B} \]

Where \(A = 10\), \(B=5\), \(C=2.5\)

def fun_function(x):
    result = ...
    return result

Now evaluate the function for \(x = 62.5\),

fun_output = ...
print(fun_output)

Python: Introduction to plotting

Code 
import numpy as np
import matplotlib.pyplot as plt

There are many ways to plot, we will be using the matplotlib library - but the concepts are similar across most ways of plotting.

We can make a plot of a straight line between two points \((x_1, y_1)\) and \((x_2, y_2)\) like so;

x = np.array([1, 2]) # This array contains all the x-coordinates
y = np.array([0, 1]) # And this contains all the y-coordinates.
fig, ax = plt.subplots(figsize=(6, 4))
ax.plot(x, y)

Note

ax is a special type (like int, float, str), you can think of it as the box that contains the plot.

If we want to connect to a third point \((x_3, y_3)\) we would instead write

x = np.array([1, 2, 2.5])
y = np.array([0, 1, 2])
fig, ax = plt.subplots(figsize=(6, 4))
ax.plot(x, y)

Notice that with three sets of points we plot two line segments.

(a) Trying to plot a square

Make a plot with lines between the following 4

  • \(P_1 = (0, 0)\)
  • \(P_2 = (1, 0)\)
  • \(P_3 = (1, 1)\)
  • \(P_4 = (0, 1)\)

Start by defining an array for both x and y

x = np.array([...]) # Replace ... with your code
# Do the equivalent for y

Now use ax.plot to make the plot

fig, ax = plt.subplots(figsize=(5, 5))
... # Replace with your code.
ax.axis('equal')
ax.set_xlim([-0.5, 1.5]) # Tells matplotlib to show us the region between -0.5 and 1.5 on the x-axis.
ax.set_ylim([-0.5, 1.5])

Consider the following;

  • Why is it not a square?
  • How many points did you use?
  • How many line segments were plotted?

(b) Actually plotting a square

In order to actually plot a square you will need to update x and y, they both need to contain five numbers such that four line segments are plotted.

x = np.array([...]) # Replace ... with your code
# Do the equivalent for y

Copy your code for making the plot from the previous exercise to the cell below

... # Put your copied code here.

(c) Plotting a function

Often the data we plot can broadly be thought of as originating from a function, that is we have

\[ y = f(x) \]

Where \(f\) is the function, this might for example be an experiment that produces some output \(y\) given some input \(x\) or it might be a traditional mathematical function like \(y = x^2\). Plotting this type of data is exactly the same as plotting a square - it just usually consists of many more data points resulting in many line segments producing a smooth looking curve.

Make a plot of the function

\[ y = \mathrm{e}^x \]

x = np.linspace(0, 5, 50) # Make 50 points uniformly between 0 and 5. 
y = ... # Your code here.

fig, ax = plt.subplots(figsize=(6, 4))
... # Your code to plot here

Once you’ve made the plot try changing the number of points in x by changing the last argument in the call to np.linspace.

  • What happens if you have very few points?
Tip

Remember that np.exp is used to calculate the exponential function.

(d) Plotting multiple functions

Often we want to plot multiple functions in the same figure as it enables us to compare them. Luckily, this is quite simple!

Plot the function

\[ y = \mathrm{e}^{ax} \]

With \(a = \left[1, \cfrac{1}{2}, 1.2\right]\) in the same plot producing three curves.

x = np.linspace(0, 5, 50) # Make 50 points uniformly between 0 and 5. 
y1 = ...
y2 = ...
y3 = ...

fig, ax = plt.subplots(figsize=(6, 4))
ax.plot(x, y1)
ax.plot(x, y2) # To plot a second curve we just use ax.plot again
... # Plot the the third curve.

(e) Customizing plots

We will generally need to customize plots a little bit, for example the plot from the previous exercise doesn’t have a label for the axis, there’s no way of telling which curve is which and it has no title.

To add labels to the x and y axis we use the two functions

  • ax.set_xlabel('String with the name of the x-axis')
  • ax.set_ylabel('String with the name of the y-axis')

Adding information about the curves we plot can be done by also giving them a label, that is done as an argument to the ax.plot call, like so

fig, ax = plt.subplots()

1ax.plot(x, y, label='Information about the curve.')
2ax.legend()
3ax.set_title('Title of plot')
1
The label argument is given when the curve is plotted.
2
ax.legend() is called to tell matplotlib to show the a ‘legend’ containing the label of all the plots that have been given one.
3
Sets the title of the plot

Copy your code from the previous exercise and add labels for both the x and y axis aswell as each curve, for example you can label them according to the value of the the parameter \(a\) like a = 1 etc.

... # Put some code here and try customizing it.
Ellipsis
Note

There are many other customization options that can be added in the same way as the label, that is

ax.plot(x, y, option_name=option_value)

Some useful examples are

  • linestyle: Controls if the plot is made using a full, dashed or dotted line using -, -- and : respectively. So ax.plot(..., ..., linestyle = ":") produces a dotted line.
  • color: Controls the color of the line - valid options are listed here https://matplotlib.org/stable/gallery/color/named_colors.html
  • linewidth: Sets the width of the line - can be any number.
  • alpha: Controls the transparency of the plot 0 being fully transparent and 1 being fully visible.

You can try some of these options for the plot you’ve made above if you want to. There are many other ways of customizing plots for different situations. The matplotlib gallery shows a number of them.

(f) Other types of plots: Scatter

Sometimes we don’t want to connect each point with a line segment but just show the points in a scatter plot.

The next cell makes some data

x = np.random.uniform(low=0, high=10, size=100)
y = 2*x + np.random.normal(scale=2, size=100)

Try plotting it like for the previous exercises

# Put your code to quickly plot in this cell - no customization needed!

You will see a very strange plot like when you scribble out a word on a piece of paper. Clearly a line plot is not a very good way of showing this data! There are, at least, two ways of making a scatter plot

  • ax.plot(x, y, 'o'): Quick and dirty way of just showing the points and not the lines.
  • ax.scatter(x, y): Function specifically for making these types of plots - with its own set of customization arguments.

Try either, or both, of these ways in the cell below

fig, ax = plt.subplots()

# Your code here.

Average properties of amino acids and proteins.

Code 
import numpy as np

In the accompanying Excel file (averag-prope-amino-acids.xlsx), you will find a table that contains the molecular weight of the 20 common amino acid residues, i.e. their weight as residues in a peptide chain. Additionally, you will find their relative frequency in E. coli proteins, where a frequency of 0.01 means that this residue constitutes 1 % of the residues in a protein.

(a) Load the data file.

Use the widget below to load the averag-prope-amino-acids.xlsx file.

from IPython.display import display 
from fysisk_biokemi.widgets import DataUploader
uploader = DataUploader()
uploader.display()

The command below will display the table as a DataFrame.

df = uploader.get_dataframe()
display(df)

(b) Average molecular weight

Calculate the average molecular weight of a residue in a protein. To do this our procedure will be as follows

  1. First calculate the residue weight times its frequency in proteins for each residue.
  2. Sum these together to get the average molecular weight.

In the cell below finish the calculation of weight_times_freq by extracting the "MW of AA residue"-column and "Frequency in proteins" and multiplying them together.

Tip

You can index in the dataframe by using the column name, for example to get the "MW of AA residue"-column you would do

col = df["MW of AA residue"]

Arrays also allows us to operate on every element in the array at the same time, so arrays can be added, subtracted, multiplied, divided, etc, see for example this figure

weight_times_freq = ...
Tip

You can use np.sum to sum all values in an array. For example

array = np.array([1, 2, 3, 4, 5])
sum_of_array = np.sum(array) # Gives 15 
average_mw = ...
print(f"{average_mw = :.3f}")
Note

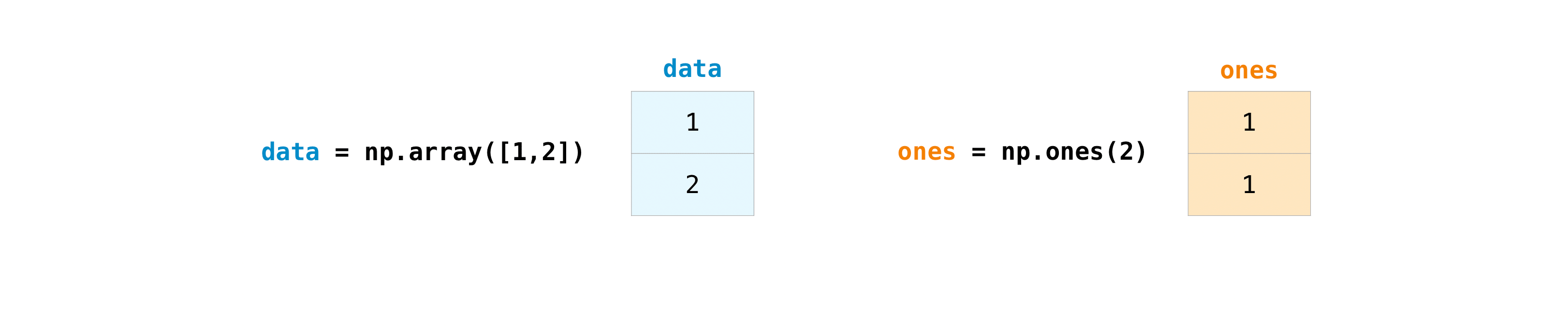
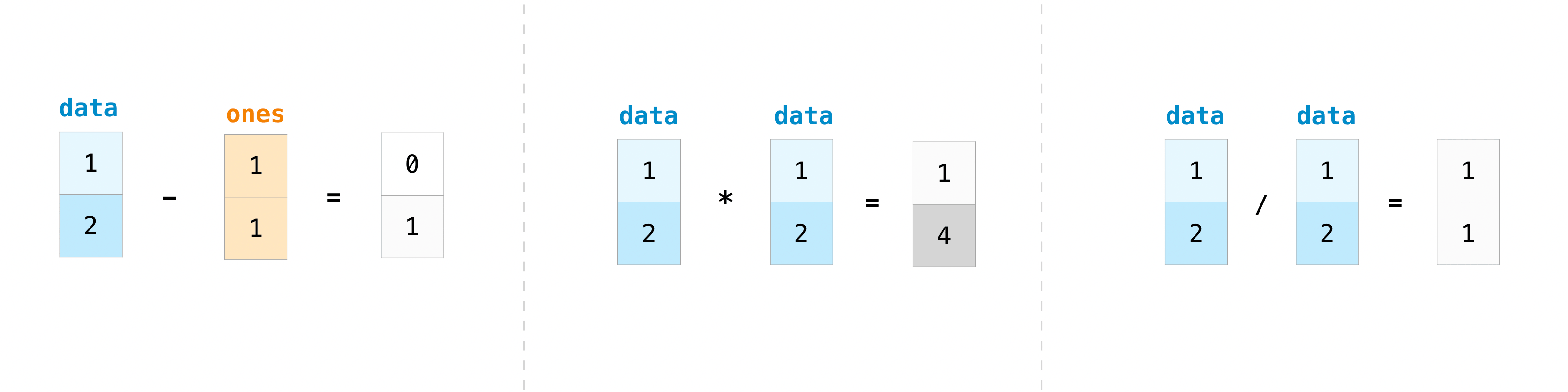
The syntax f"{average_mw = :.3f}" is just a way of printing the value with a nicer format, in this case we print the value to 3 decimal places. In Python these are called f-strings, you don’t need to understand the details at the moment.

(c) Weight of 300-residue protein

What would the molecular weight of a 300-residue protein most likely be, if you did not know its sequence?

mw_300 = ...
print(f"{mw_300 = :.3f}")

In many projects, you will be working with a mixture of proteins. This could for example be a cell lysate or a biological fluid for protein abundance analysis, or the early stages of a protein purification process. In these situations, you cannot work with a molecule specific extinction coefficient. Instead, we would use the average values, which we will determine below.

(d) Average concentration of residues

Calculate the average concentration of amino acid residues in a protein mixture at 1 mg/mL.

c_residue_avg = ...
print(f"{c_residue_avg = :3.3f} M")

(e) Absorbance

Calculate the absorbance from such a mixture under the assumption that only Trp and Tyr contribute.

freq = df.set_index("Name")["Frequency in proteins"]
f_trp = freq["Tryptophan (Trp/W)"]
f_tyr = freq["Tyrosine (Tyr/Y)"]
c_trp = ... # Erstat med din kode.
c_tyr = ... # Erstat med din kode.

print(f"{c_trp = :3.5f}")
print(f"{c_tyr = :3.5f}")
A280 = ... # Erstat med din kode.
print(f"{A280 = :3.3f}")

(f) Adsorbance \(\rightarrow\) concentration

For a cell lysate, you measure and absorbance of 0.78 at a path length of 0.5 cm. What is the protein concentration?

# Set known values:
A = 0.78 # Unitless
l = 0.5 # cm

# Extract frequencies
freq = df.set_index("Name")["Frequency in proteins"]
f_trp = freq["Tryptophan (Trp/W)"]
f_tyr = freq["Tyrosine (Tyr/Y)"]

# Calculate extintinction coefficent in [L/(mol cm)]
eps_mix = ...
# Calculate molar concentration [mol/L]
c_res = ...
# Calculate concentration [g/L] = [mg/mL]:
conc_mg_per_mL = ...
print(f"Protein concentration = {conc_mg_per_mL:.3f} mg/mL")

UV spectrum of apo- and holo-myoglobin

Code 
import matplotlib.pyplot as plt

In this exercise we will analyze the spectra of apo- and holo-myoglobin. The dataset is given in uv-spec-apo-holo-myo.csv.

(a) Load the dataset

Use the widget to load the dataset.

from IPython.display import display 
from fysisk_biokemi.widgets import DataUploader
uploader = DataUploader()
uploader.display()

Run this cell after having uploaded the file in the cell above.

df = uploader.get_dataframe()
display(df)

(b) Plot the spectra

Using matplotlib plot each spectrum in the same figure as line plots.

fig, ax = plt.subplots() 

# This selects the 'holo_absorbance'-column and plots it
ax.plot(df['wavelength'], df['holo_absorbance'], label='Holo')

# Copy the line above and edit it to also plot the Apo absorbance
... # Your code here

ax.set_ylabel('Absorbance (AU)')
ax.set_xlabel('Wavelength (nm)')

Based on the spectra explain what ApoMb and HoloMb represent?

You have learned that pure proteins without any UV/Vis-absorbing prosthetic groups bound, have basically no absorbance at wavelengths above λ>320 nm. Nevertheless ApoMb still show some absorbance above 320 nm. In this case, it can explained by the fact that ApoMb was generated from HoloMb by a procedure that will not be explained here.

(d) Adsorption above 320 nm.

Explain why ApoMb in the spectrum above absorbs light at λ>320 nm.

(e) Efficiency estimate.

Give a rough estimate of the efficiency of the chosen procedure of heme-group removal.

(f) Isobestic points

Are there any isobestic points between the two spectra?

To get a better understanding of the causes for the different spectra, you can compare to litterature. The figure below shows the absorbance spectra of three states of myoglobin.

\[ \begin{aligned} \mathrm{MbFe(II)O_2} &\Rightarrow \mathrm{oxyMb} \\ \\ \mathrm{MbFe(III)} &\Rightarrow \mathrm{metMb} \\ \\ \mathrm{MbFe(II)} &\Rightarrow \mathrm{deoxyMb} \end{aligned} \]

Absorbance spectra of different states of myoglobin. \mathrm{MbFe(II)O}_2 is “oxyMb”, \mathrm{MbFe(III)} is “metMb” and \mathrm{MbFe(II)} is “deoxyMb”. Taken from Barham et al (2010); ChemRev; 110 (4); pp2313-2365

Absorbance spectra of different states of myoglobin. \(\mathrm{MbFe(II)O}_2\) is “oxyMb”, \(\mathrm{MbFe(III)}\) is “metMb” and \(\mathrm{MbFe(II)}\) is “deoxyMb”. Taken from Barham et al (2010); ChemRev; 110 (4); pp2313-2365

(g) Aged myoglobin

metMb \((\mathrm{MbFe(III)})\) is normally described as ‘aged’ myoglobin. What does this mean in terms of the bound iron?

(h) Change in absorbance

Give a qualitative explanation to the observed change in absorbance of metMb compared to fresh oxy-/deoxyMb?

(I) Type of shift

Is the spectral difference from deoxyMb to metMb a redshift or a blueshift?

(J) Experiment design

You would like to set up an experiment where the absorbance of myoglobin at defined wavelength(s) should be used to measure the level of \(\mathrm{O}_2\) binding. Sketch how the absorbance spectra would look like when going from deoxyMb and continuously increasing the concentration of \(\mathrm{O}_2\) (draw this for five different \(\mathrm{O}_2\) concentrations going from pure deoxyMb to pure oxyMb)

Proteins in blood plasma.

In this exercise we will learn how Python is excellent for handling datasets with many data points and how it can be used to apply the same procedure to all the data points at once.

A researcher wants to determine the concentration of two proteins in blood plasma that is suspected to be involved in development of an autoimmune disease. 500 patients and 500 healthy individuals were included in the study and absorbance measurements of the two purified proteins from all blood plasma samples were measured at 280 nm. The molecular weight and extinction coefficients of the two proteins are given in the table below.

Properties of the two proteins.
Protein \(M_w\) \([\text{kDa}]\) \(\epsilon\) \([\text{M}^{-1}\text{cm}^{-1}]\)
1 130 180000
2 57 80000

(a) Load the dataset

Use the widget to load the dataset as a dataframe from the file protei-blood-plasma.xlsx

from IPython.display import display 
from fysisk_biokemi.widgets import DataUploader
uploader = DataUploader()
uploader.display()

Run this cell after having uploaded the file in the cell above.

df = uploader.get_dataframe()
display(df)

(b) Calculate concentrations

Calculate the molar concentration of the two proteins in all samples, the light path for every measurement is 0.1 cm.

Always a good idea to assign known values to variables

protein_1_ext_coeff = 180000
protein_2_ext_coeff = 80000
l = 0.1
Tip

You can set new columns in a DataFrame by just assigning to it

df['new_column'] = [1, 2, 3, ..., 42]

It can also be set as a computation of a property from another row

df['new_column'] = df['current_column'] / 4
df['protein1_healthy_molar_conc'] = ... # Calculate for concentration in healthy for protein 1.
... # Your code that updates the data frame with the 3 other new columns.
display(df)

(c). Concentrations in mg/mL

Add another set of four columns containing the concentrations in mg/mL.

protein_1_mw = 130 * 10**3
protein_2_mw = 57 * 10**3
df['protein1_healthy_conc'] = ...
df['protein1_patient_conc'] = ...
df['protein2_healthy_conc'] = ...
df['protein2_patient_conc'] = ...

names = ['protein1_healthy_conc', 'protein1_patient_conc', 'protein2_healthy_conc', 'protein2_patient_conc']
display(df[names])

(d) Mean concentration

Now that we have the concentrations, calculate the concentration in the four categories.

Tip

When displaying the dataframe above we used indexed it with names as df[names]. We can do the same to compute something over just the four rows.

For example the if we have a DataFrame called example_df, we can calculate the mean over the rows as:

df[names].mean(axis=0)

Here axis=0 means that we apply the operation over the first axis which by convention are the rows. The figure below visualizes this

mean = ...
display(mean)

(e) Standard deviation

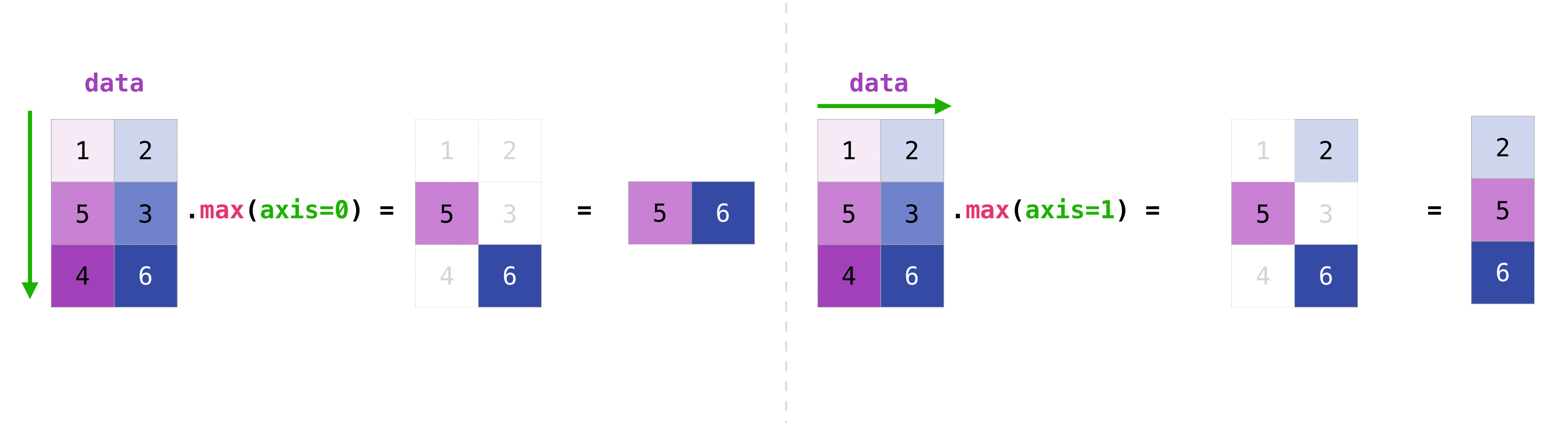
Calculate the standard deviation

Tip

The standard deviation can be calculated using the .std-method that works in the same way as the .mean-method we used above.

std = ...
display(std)

(f) Analyze the results

Consider the following questions

  • By comparing healthy individuals with patients, would you expect that any of the two proteins would be involved in disease development?
  • What additional information does the standard deviation provide besides the average value of the protein concentration?

The fluorescent protein “mCherry”.

The spectra of many fluorescent proteins can be found at the website: www.fpbase.org. Go to FPbase and search for “mCherry”.

(a) Find parameters.

Find the following parameters for the protein

  • Extinction coefficient at absorbance maximum
  • Quantum yield
  • The organism from which it was originally isolated
  • Molecular weight

Save them to seperate variables in the cell below.

... # Your answers here.

(b) Adorbance

What is the absorbance of a 1 µM solution of mCherry at its absorption maximum?

c = ... # Put the concentration in Molar
l = ... # Path length in cm
A_max = ... # Calculate the adsorbance.
print(f"{A_max = :3.3f}")

(c) Extinction coefficient from sequence.

The sequence of the protein is also given. From this determine the extinction coefficient at 280 nm.

Start by taking the sequence from the website and assigning it to the variable sequence in the cell below.

sequence = ... # Your code here

Now use the sequence to calculate the extinction coefficient, finish the code below (or take the function you implemented in a previous exercise!)

# This is "dictionary" with the extinction coefficients of the relevant 
# amino acid residues. Dictionaries are indexed with 'keys', so you can retrieve
# the value for W as: ext_residue["W"].
ext_residue = {"W": 5500, "Y": 1490, "C": 125}

# Write code to calculate the extinction coefficent
...
Ellipsis

(d) What is the concentration of a 1 µM solution of mCherry in mg/mL?

conc_molar = ... # Put the concentration in units of M. 
conc_mg_mL = ... # Calculate the concentration in uts of mg/mL.
print(f"{conc_mg_mL = }")

The excitation and emission spectra can be downloaded as a csv-file by clicking the download icon as highlighted below

Figure 1: Screenshot of the download button on fpbase

(e) Load the dataset

Use the widget below to load the dataset as a DataFrame

from fysisk_biokemi.widgets import DataUploader
from IPython.display import display 
uploader = DataUploader()
uploader.display()

Run the next cell after uploading the file

df = uploader.get_dataframe()
display(df)

(f) Plot spectra

Make your own plot showing the excitation and emission spectra of “mCherry” using the above data.

Tip

To plot we use the matplotlib package. Plots are generally just straight lines connecting points, with enough points we get a smooth looking figure.

For example, to plot a line connecting three datapoints

1fig, ax = plt.subplots()

2x = np.array([1, 2, 3])
y = np.array([1, 4, 9])
3ax.plot(x, y)
4plt.show()
1
This creates a fig and an ax, the ax-object is the box where our plot is created.
2
Define the data to put on the x-axis.
3
Does the actual plotting
4
Shows the figure

There are many ways of customizing plots, you will see different ones in the exercises, but by no means all of them - if you are interested you can find more information on the matplotlib documentation.

You don’t have to worry about the NaN values in the dataset when plotting, matplotlib just skips plotting that line segment.

import matplotlib.pyplot as plt
fig, ax = plt.subplots(figsize=(9, 4))
ax.plot(..., ..., label='Excitation') # Replace ... with your code
... # Replace ... with your code plotting the emission spectrum.
ax.legend()
ax.set_xlabel('Wavelength')
ax.set_ylabel('Extinction & Emission')
plt.show()

(g) Stokes shift

What is the Stokes shift of mCherry?

Tip

If you have two arrays A and B you can find the entry in A corresponding to the largest value in B like this

A_at_B_max = A[np.argmax(B)]

The np.argmax stands for argument maximum meaning that it finds the index of the maximum value in a given array. The figure below illustrates this

Figure 2: Illustration of argmax 
import numpy as np
# Start by extracting the wavelengths from the DataFrame
wavelengths = ...

# Find the indices
ex_max_idx = np.argmax(...)
em_max_idx = ...

# Use the index to find the corresponding wavelengths
lambda_ex = wavelengths[...]
lambda_em = ...

stokes_shift = ...

print(f"{lambda_ex = :d}")
print(f"{lambda_em = :d}")
print(f"{stokes_shift = :d}")

(h) Colors

What colors are the light that correspond to the excitation and emission maxima respectively?

Tryptophan absorption and fluorescence

from fysisk_biokemi.datasets import load_dataset
from IPython.display import display
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
pd.set_option('display.max_rows', 6)

You investigate a protein that neither contains tyrosine nor cysteine residues. A 37 µM solution gives an absorbance of 0,41 at 280nm at a light path of 1 cm.

(a) Number of residues

How many tryptophan residues does the protein contain?

(b) Concentration

You would like to conduct a protein stability experiment at an absorbance of 0,8 (path length 1cm). What concentration should you use?

(c) Spectra & Stokes Shift

The cell below loads extinction and emission spectra for tryptophan in aqueous buffer. (The data files are trypt-absor-fluor-emission.xlsx and trypt-absor-fluor-extinction.xlsx)

df_emission = load_dataset('week47_1_emi')
df_extinction = load_dataset('week47_1_ext')
display(df_emission)
display(df_extinction)
wavelength_(nm) emission_(AU)
0 280.0 379
1 280.5 396
2 281.0 403
... ... ...
396 478.0 5024
397 478.5 4950
398 479.0 4813

399 rows × 2 columns

wavelength_(nm) molar_extinction_(cm-1/M)
0 219.75 12488
1 220.00 12872
2 220.25 12428
... ... ...
396 318.75 14
397 319.00 18
398 319.25 45

399 rows × 2 columns

print(df_extinction.keys())
Index(['wavelength_(nm)', 'molar_extinction_(cm-1/M)'], dtype='object')

Make plot showing the two spectra and determine the Stokes shift.

fig, axes = plt.subplots(1, 2, figsize=(7, 3), layout='constrained')

# Emission 
ax = axes[0]
ax.set_title('Emission')

# Replace ... with your code.
ax.plot(..., ..., label='Emission', color='C0')

ax.set_ylabel('Emission')
ax.set_xlabel('Wavelength [nm]')

# Extinction
ax = axes[1]
ax.set_title('Extinction')

# Replace ... to plot the extinction spectrum
...

ax.set_ylabel('Extinction')
ax.set_xlabel('Wavelength [nm]')
plt.show()

Recall that we have used np.argmax to determine the maximum index before, use that to calculate the Stokes shift

max_index = np.argmax(...) # Replace ... to get the index of the maximum of the emission spectrum
emission_wavelength_max = df_emission['wavelength_(nm)'][max_index]

max_index = ... # Replace ... to get the index of the maximum of the extinction spectrum
extinction_wavelength_max = df_extinction[...][...] # Use the index to get the wavelength at of the maximum.

print(f"{emission_wavelength_max = :.1f} nm")
print(f"{extinction_wavelength_max = :.1f} nm")

(d) pH and how it changes pHroperties.

Next, you compare the fluorescence emission spectra for your protein at pH 7 and at pH 2. You can find the data in the files trypt-absor-fluor-ph2.xlsx and trypt-absor-fluor-ph7.xlsx - the cell below also loads these datasets

df_ph2 = load_dataset('week47_1_ph2')
df_ph7 = load_dataset('week47_1_ph7')
display(df_ph2, df_ph2)
Wavelength(nm) Fluo_Int
0 311.623037 0.890000
1 314.450262 1.128668
2 315.863874 1.128668
... ... ...
43 367.068063 27.990971
44 368.638743 27.313770
45 370.052356 26.636569

46 rows × 2 columns

Wavelength(nm) Fluo_Int
0 311.623037 0.890000
1 314.450262 1.128668
2 315.863874 1.128668
... ... ...
43 367.068063 27.990971
44 368.638743 27.313770
45 370.052356 26.636569

46 rows × 2 columns

Make a plot comparing the two emission spectra. Which resembles the spectrum of tryptophan in water most?

fig, ax = plt.subplots()

ax.plot(..., ..., label='pH = 2') # Replace to plot at pH = 2
... # Replace to plot at pH = 7

ax.set_xlabel('Wavelength [nm]')
ax.set_ylabel('Flouresence [AU]')
plt.show()

(e) for Explain

Explain why the same protein gives such different spectra at pH 2 and pH 7.  

Extinction coefficient of human myoglobin

The protein of human myoglobin is given below

sequence = """GLSDGEWQLVLNVWGKVEADIPGHGQEVLIRLFKGHPETLEKFDKFKHLKSEDEMKASEDLKKHGA
TVLTALGGILKKKGHHEAEIKPLAQSHATKHKIPVKYLEFISECIIQVLQSKHPGDFGADAQGAMNKALELFRKDMASNY
KELGFQG"""

We want to calculate the extinction coefficient of this protein, we have seen that this can be calculated using the formula

\[ \epsilon(280 \mathrm{nm}) = N_{Trp} \epsilon_{Trp} + N_{Tyr} \epsilon_{Tyr} + N_{Cys} \epsilon_{Cys} \tag{1}\]

Where \(N_{Trp}\) is the number of Tryptophan in the protein (and likewise for the other two terms), and the three constants \(A\), \(B\) and \(C\) are given as

\[ \begin{align} \epsilon_{Trp} &= 5500 \ \mathrm{M^{−1} cm^{−1}} \\ \epsilon_{Tyr} &= 1490 \ \mathrm{M^{−1} cm^{−1}} \\ \epsilon_{Cys} &= 125 \ \mathrm{M^{−1} cm^{−1}} \end{align} \]

In order to calculate the formula we need to know the count of the relevant residues, we can use Python to get that - for example we can count the number of Tryptophan like so;

N_trp = sequence.count("W")

(a) Determine the number of residues

In the cell below find the number of residues

N_tyr = ... # Your code here
... # Your code here for the N_cys.

You can check what Python has stored each variable by using print

print(N_trp)
print(f"{N_tyr = }") # This is just a way of make a string that looks nice.
print(f"{N_cys = }")
2
N_tyr = 2
N_cys = 1

(b) Calculate the extinction coefficient

Use equation (Equation 1) to calculate the extinction coefficient of human myoglobin.

eps_trp = 5500
eps_tyr = 1490
eps_cys = 125
epsilon = ... # Erstat ... med din kode.
print(epsilon)

What are the units of this value?

(c) Compare residue count to ProtParam

ProtParam is an online tool that calculates various physical and chemical parameters from a given protein sequence and is used worldwide in research laboratories.

Protpram tool input page.

Protpram tool input page.

Go to ProtPram at this link: https://web.expasy.org/protparam/ and paste the sequence and click Compute Parameters. You should then see the calculated parameters, similar to in the image below

Protpram tool calculated properties.

Protpram tool calculated properties.

On the output page you will see the number of residues, does that match your calculation?

(d) Calculate the absorbance

Using the extinction coefficient and the molecular weight given by ProtParam, calculate the absorbance at 280 nm of a myoglobin solution at a concentration of 1 mg/mL in a cuvette with a light path of 1 cm.

molecular_weight = ... # Find the value on ProtPram (It has units of g/mol)
path_length = ... # Set the value of the path length
concentration = ... # Set the value of the concentraiton.

Remember to convert the concentration to \(\mathrm{mol/L}\).

A280 = ...
print(A280)

This value is what is known as the A280(0.1%) of a protein, i.e. the absorbance of a given protein at a concentration of 0.1% weight/volume (= 1 g/L = 1 mg/mL).

(e) Tintin

We have now calculated the extinction coefficient of a protein, now we will make our code more reusable so that it can be applied to other proteins easily.

Note

A function in Python is a set of instructions, like a recipe, that can be defined and reused multiple times. The syntax is like this

1def my_function(input_1, input_2):
    # Some operation 
2    some_internal_variable = input_1 + input_2
    ... 
3    return something_weve_calculated
1
The def command is used to define the functions name, here my_function, and state its inputs, e.g. the name and ingredients of a recipe.
2
The body of the function defines what it does, the body can have any number of lines of code. Similar to the instructions of a recipe.
3
Finally, the function can return something, like the final product of a recipe.

Note that the function is not executed by doing this, like how a cake isn’t baked by writing down the recipe, in order actually use the function it needs to be called

output = my_function(1, 2)

This is also how we have already used other functions like print.

The way of doing so is by defining a function that does the necessary operations for a given sequence. In this way the code can be reused for any sequence.

Finish implementing the body of the function below, note that you have already written all the required code - you just need to copy it into the function.

def extinction_coefficient(sequence):

    # Start by counting
    ...

    # Define the residue extinction coeffiecients
    eps_trp = 5500
    eps_tyr = 1490
    eps_cys = 125

    # Calculate 
    epsilon = ...

    return epsilon

It’s always a good idea to check that functions do what we expect, so we can confirm that it gives the same result for human myoglobin as we calculated before

epsilon_func = extinction_coefficient(sequence)
print(f"Epsilon: {epsilon}")
print(f"Epsilon from function: {epsilon_func}")

The largest known protein is Titin, the cell below loads the sequence of titin and prints a few bits of information about it. (You can also find the full sequence in the dataset extin-coeff-human-myogl.txt.)

from fysisk_biokemi.datasets import load_dataset
titin_sequence = load_dataset('titin')

print(f'Titin number of residues: {len(titin_sequence)}')
print('First 100 residues')
print(titin_sequence[0:100])

Use your function to calculate the extinction coefficient of titin.

titin_eps = ... # Your code here. 
print(titin_eps)
Tip

You don’t need to understand the code below, it’s just ment to illustrate that knowing some Python will allow you to explore the topics that interest you in more detail.

In general Python is very powerful at letting us explore properties of sequences, for example the cell below calculates number of residues between each Tryptophan in the Titin sequence and plot the distribution.

import numpy as np
import matplotlib.pyplot as plt

def get_distance(sequence, letter):
    W_index = np.argwhere(np.array([l for l in sequence]) == letter)
    count = len(W_index)
    distance = (W_index - np.roll(W_index, 1))[1:]
    return distance, count

letters = ['W', 'Y', 'C']

fig, axes = plt.subplots(1, 3, figsize=(3*3, 3), sharey=True)
axes = axes.flatten()

for ax, letter in zip(axes, letters):
    distance, count = get_distance(titin_sequence, letter)
    ax.hist(distance, bins=np.arange(0, 500, 25), 
        edgecolor='black', alpha=0.75, density=True)
    ax.set_xlabel('Distance [Number of residues]')
    info = f'Residue: {letter} \nCount: {count} \nMean distance: {np.mean(distance):.1f}'
    ax.text(0.975, 0.975, info, transform=ax.transAxes, ha='right', va='top')